为什么神经网络会存在灾难性遗忘(catastrophic forgetting)这个问题？

所谓灾难性遗忘，就是一个在原始任务上训练好的神经网络在训练完新任务后，在原始任务上的表现崩溃式的降低。

目测灾难性遗忘会成为一个非常关键热门的问题。毕竟连GPT4都无法解决这个问题…今后和语言相关的模型必然是基于某个Foundation Model微调或生长出多任务的Head，视觉模型目测也会这样。灾难性遗忘将成为绕不过去的灾难。。。

有很多角度来看待，最近看了篇综述，就文末那篇，写得很好的，我就把那论文当原材料，再加上一些我额外了解的新论文，极致简化+重新编织一下思路。

微观视角-权重

最粗暴最直接的：观察权重变化。为什么会遗忘？神经元的权重被修改了嘛，如果某些权重对原始任务很重要，那经过新任务训练，你无法保证这些权重不被修改。一旦权重被动了，那就无法保证原始任务的performance。

小心翼翼地调整权重

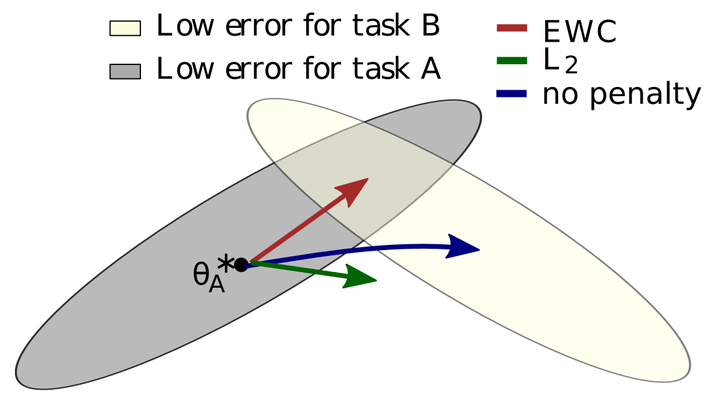
所以最简单的想法就是把这些权重保护起来，或者修改的时候小心翼翼的改。做法有很多，比如著名的EWC：

图中的权重原本是在A任务被训练的，已经位于A任务的舒适区（灰色）了，现在却要被B任务拉走，如果任由B任务控制权重，他就走蓝线去B任务舒适区（淡黄色）了。EWC可以让权重走红线，在不离开A任务舒适区的情况下仍然可以靠近B任务舒适区。

将重要的权重冻结

还有一个想法更加粗暴，根据Lottery tickets hypothesis那篇论文，神经网络里只有一部分权重真正起作用，很多都是没用的。那我们只需要把这些重要的权重挖出来，然后保护起来谁都不许碰就可以了。找关键权重的过程其实就是网络压缩，于是就出现了下面这个基于网络压缩的算法PackNet：

就是经过原始任务训练后，进行网络压缩之后把重要的权重冻结起来，然后利用那些对原始任务没

用的权重训练新任务。

那显然万一挤出来能用的权重不够怎么办？很容易想到的做法—权重不够，malloc来凑嘛！于是就出现了各种动态扩张网络来容纳新任务的论文。

仿生学视角-人的遗忘和记忆

根据仿生学来理解也是很自然的。因为人也是会遗忘的（不是灾难性的），人遗忘的原因还没有定论。但人防止遗忘的方法大家都懂：复习。

复习

所以就出现了大量基于复习的算法，最简单的，基于样本复习，就是训练新任务的时候混一些旧任务的数据样本。我们有时候复习就不看整本教科书了，就只复习划线部分，在这也一样，可以提取一个小的精华数据集，专门用于复习…

还有就是基于特征记忆的复习。人的记忆并不是集中存在一个地方，而是分散存放的，有的记忆并不是细节，是抽象过的，模糊的。比如你可能记得天安门的大概轮廓，但具体细节就记不清了。那么时不时的回忆下天安门的轮廓，也有助于防止遗忘。这个REMIND算法就是这个原理：

专门把特征图存起来，量化以后放在一个类似于记忆库的地方，之后在新任务上训练的时候从这个记忆库里重构出记忆和新数据一起训练。

模拟睡眠

神经科学研究表明，睡眠对巩固人的记忆非常重要。而睡眠巩固记忆的方法是大脑自己放电，激活和强化某些神经连接，起到巩固记忆的目的。等于是一种随机的复习。

这篇自然-通讯杂志的文章，提出了一个叫睡眠重播固化（Sleep Replay Consolidation (SRC)）的算法，对一个神经网络模拟睡眠。方法超级简单，就是给一个神经网络输入噪音信号，这些噪音信号激活的连接往往和原始任务有关，直接强化这些连接就可以了。具体我也没深究，为了模拟睡眠，在睡眠阶段他们把神经网络模型变换成了一个SNN（Spiking Neural Network）。不可能真的用这个方法，但很有意思：

优化算法视角

从优化角度理解也很直观，下面是两个不同任务的损失曲面，现在假设上面那个大片片的任务训练完了，要在下面那个很多丘陵的任务上继续训练：

两个损失曲面示意图，蓝色箭头是当前点在原任务上的梯度，红色箭头是新任务上的梯度，蓝色轨迹为走红色路线后投影在原任务损失面上的轨迹。

然后你会发现，当前所在的点可能位于第一个任务的底部了，但却位于第二个任务的山峰上，你如果照着第二个任务的梯度（红色箭头）滑下去，第一个任务的损失越爬越高，那立马就挂了，这就是灾难性遗忘。

那么怎么克服这个问题？

找到一个平坦区域

如果位于第一个任务的平坦区域，那么即便第二个任务再野，也不会影响第一个任务，这个很好理解吧。说白了就是训练一个泛化性很好的模型，所有提高泛化性的手段都可以用上去。

找到连通路径

这篇论文说了，神经网络的所有的极小值其实都是连通在一起的，文章还提出了如何从一个极小值找到一条通路连到另一个极小值的算法。

那么很容易想到，我可以从原始任务的某个极小值出发，在优化新任务的时候尽量沿着底部的通道走，就可以保证原始任务不受影响了。这个算法和EWC高度类似。

考虑高维度

还有一个思路是我们考虑到神经网络的网络层是位于超高维度的，那么在优化新任务的时候，我如果保证优化的方向和原始任务不相干就可以了。所以就出现了那篇Orthogonal gradient descent果保证优化的方向和原始任务不相干就可以了。所以就出现了那篇Orthogonal gradient descent

一个低秩空间是垂直的。因为神经网络的权重维度特别高，所以实现这一点并不难。

其实你仔细想想，这和基于Prunning的方法又是很类似了，Prunning直接锁住重要的权重不动，只优化不重要的，相当于是用一个极端暴力的方法保证新任务梯度和原始任务梯度垂直。因为那些被压缩掉的权重，往往得到的梯度很少。

任务分解视角

这就是和多任务网络相关的问题了，一般是预训练一个主干网络，然后在上面连多任务head。通过新任务和预训练任务的相关性设计新任务head的大小，以及分支的stage等等。

文章来自于 知乎“刘斯坦”，作者 “刘斯坦”